Superconductivity and Quantum Computing
About the project
![]()
![]()
This repository contains Python code for analyzing data from a real-world quantum mechanics experiment. The experiment involved using liquid helium to reduce the temperature of the josephson junction to a level where Cooper pairs propagate with zero resistance.
Link to the project files: github.com/Al-1n/Superconductivity
Full scientific report: Superconductivity: Nb/AlOx/Nb Josephson Junctions
Requirements
- JupyterLab
- Pandas
- NumPy
- Lmfit
- Matplotlib
How to use this project
The code in these files can be adapted and used as a guidline for analyzing measurements of the properties predicted by the BCS theory of superconductivity using low-temperature methods and Josephson Junctions in a lab setting.
Any environment that can load a python kernel and run jupyter notebooks such as vs code, google collab or conda can be used.
In order to adapt the code to new measurements, a basic understanding on how to place, load and transform the data is required.
Contributors
The experiment was performed under the guidance of Dr. Mengkun Liu and Gleb Aminov.
The data collection team included Zachary Kluger, Justin Ao, Jeremy Schleiffer and Alin Airinei.
Background
This project focuses on testing some of the key predictions of one of the most succsessful theories in physics: the BCS theory of superconductivity. The theory is named after John Bardeen, Leon Cooper and J. Robert Schrieffer who shared the 1972 Nobel Proze in Physics for the discovery of the BCS theory. John Bardeen also shared the 1956 Nobel Prize in Physics for his contribution in the development of the first transistors at Bell Labs.

John Bardeen, Leon Cooper and Robert Schrieffer. Image credit: University of Illinois Nobel Laureats.
One year after Bardeen, Cooper and Schriffer received the Nobel prize for the BCS theory, Brian Josephson received the 1973 Nobel Prize in physics “for his theoretical predictions of the properties of a supercurrent through a tunnel barrier, in particular those phenomena which are generally known as the Josephson effects”. Below there is a summary of the key principles of superconductivity including the BCS theory.
General characteristics of superconductivity
- Critical Temperature: The transition to the superconducting state occurs below a critical temperature, Tc, characteristic to each superconductor.
- Zero electrical resistance: Superconductors will have zero electrical resistance below their critical temperature (Tc). This means that electric current can flow through a superconductor without any loss of energy.
- The Meissner effect: Superconductors will expel magnetic fields from their interiors. This is known as the Meissner effect.
- The isotope effect: The critical temperature of a superconductor is inversely proportional to the square root of the mass of its isotopes. This means that heavier isotopes will have lower critical temperatures.
With respect to the current project the isotope effect is particularly significant as we tested a Niobium based junction. Among the pure superconducting elements, Niobium has the highest Tc of 9.25K, as was first measured by Meissner in 1930.
BCS Theory
- Formation of Cooper Pairs: BCS theory predicts the existence of Cooper pairs, where electrons with opposite spins form pairs due to electron-phonon interactions.
- Flux quantization: The magnetic flux through a superconducting loop must be quantized in units of the flux quantum, which is defined as hc/2e, where h is Planck’s constant, c is the speed of light, and e is the elementary charge.
- Energy gap: There will be an energy gap between the ground state of a superconductor and the excited states. This means that it takes a certain amount of energy to excite an electron from the ground state to an excited state.
Josephson Junctions as candidates for Quantum Qubits
A Josephson junction is a type of electrical junction made of two superconductors separated by a thin insulating layer. In a superconductor, electrons flow in pairs called Cooper pairs, and these pairs can tunnel through the thin insulating layer of the Josephson junction. The current through the junction is determined by the difference in the phases of the Cooper pairs on the two sides of the junction.
At low voltages, the current through the Josephson junction is sinusoidal and its amplitude is proportional to the applied voltage. However, at higher voltages, the current becomes nonlinear and exhibits hysteresis. This nonlinearity is due to the inductance of the junction, which is a measure of its ability to store magnetic energy.
The inductance of the Josephson junction arises from the fact that the Cooper pairs flow in a loop around the junction. When a current flows through the junction, it creates a magnetic field that interacts with the Cooper pairs and causes them to flow more slowly. This reduces the current through the junction, which in turn reduces the magnetic field, and so on. This feedback loop creates the nonlinear behavior of the Josephson junction.
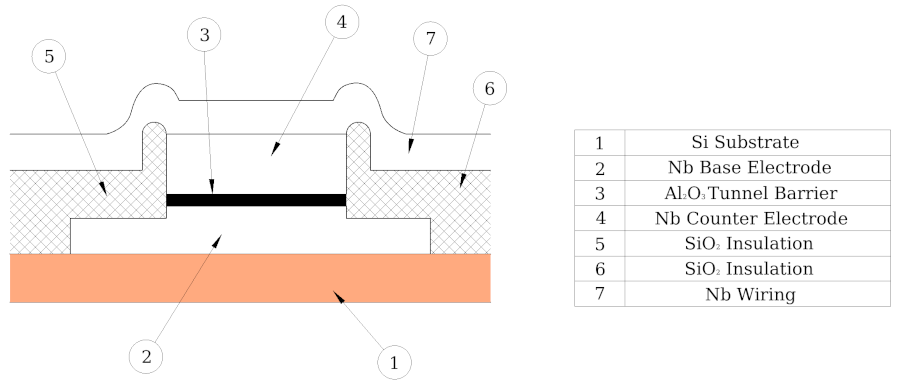
Conceptual representation of the cross-section of a NbAl2O3Nb tunneling junction.
Binary Representation and Quantum Computing
The inductive nonlinearity of the Josephson junction can be used to represent binary information. The two states of the qubit, “0” and “1”, can be represented by the two phases of the Cooper pairs in the junction. The “0” state corresponds to a phase difference of 0, while the “1” state corresponds to a phase difference of π.
The state of a qubit can be manipulated by applying a magnetic field to the junction. The strength of the magnetic field determines the phase difference of the Cooper pairs, and thus the state of the qubit.
Qubits can be entangled, which means that they are linked together in such a way that they share the same fate. Entanglement is a key feature of quantum computing, and it allows qubits to perform computations that are impossible for classical computers.
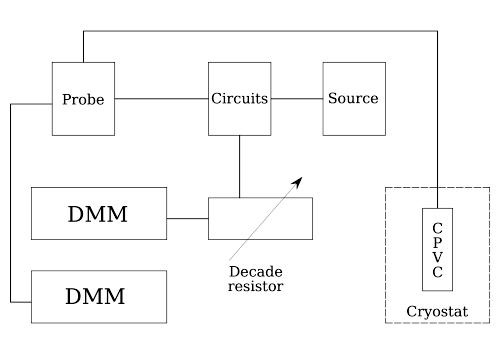
The diagram shows the temperature measuring component of the experimental setup. The Cryogenic Probe Vacuum Can (CPVC) contains enclosed the test circuitry including the germanium thermometer and the Josephson junctions.
Advantages of Quantum Computers and Superconducting Qubits
Quantum computers have several advantages over classical computers. They can solve certain problems that are intractable for classical computers, such as factoring large numbers. They can also be used to simulate complex systems, such as molecules and materials.
Superconducting qubits have several advantages over other qubit candidates. They are relatively easy to fabricate, and they have long coherence times, which means that they can maintain their quantum states for extended periods of time. Additionally, superconducting qubits can be coupled together using external magnetic fields, which facilitates the manipulation and entanglement of qubits.